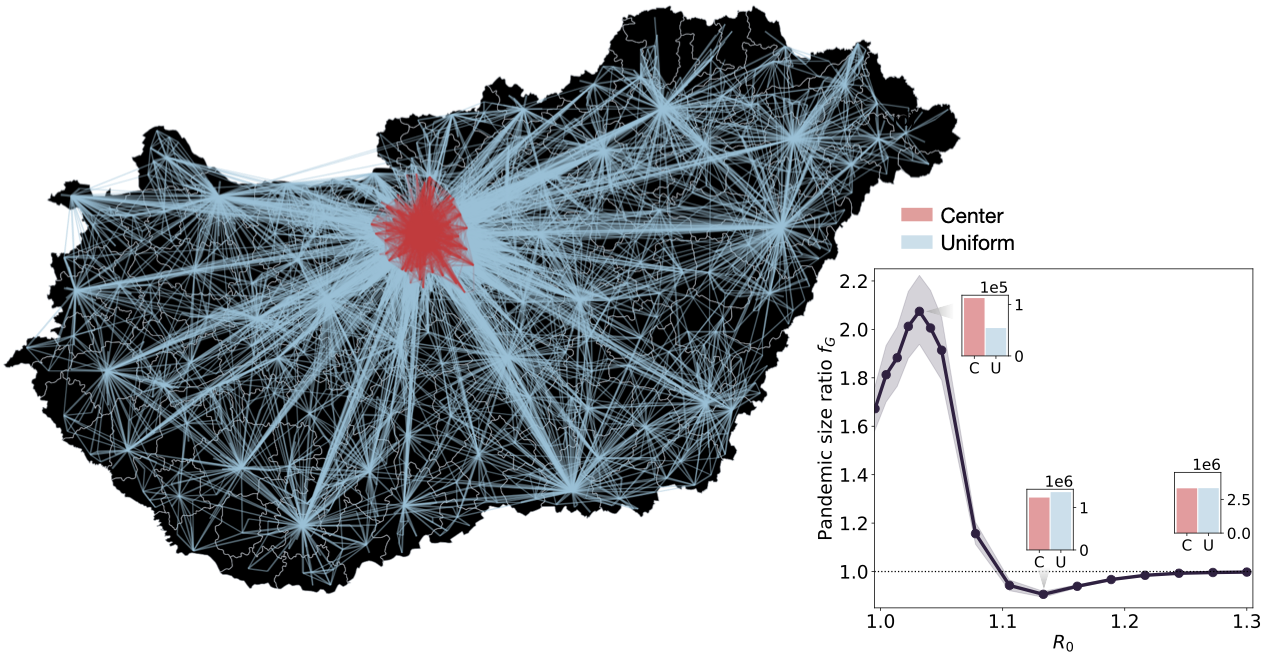
It is a fundamental question in disease modeling how the initial seeding of an epidemic, spreading over a network, determines its final outcome. One important goal has been to find the seed configuration, which infects the most individuals. Although the identified optimal configurations give insight into how the initial state affects the outcome of an epidemic, they are unlikely to occur in real life. In this paper we identify two important seeding scenarios, both motivated by historical data, that reveal a complex phenomenon. In one scenario, the seeds are concentrated on the central nodes of a network, while in the second one, they are spread uniformly in the population. Comparing the final size of the epidemic started from these two initial conditions through data-driven and synthetic simulations on real and modeled geometric metapopulation networks, we find evidence for a switchover phenomenon: When the basic reproduction number \(R_{0}\) is close to its critical value, more individuals become infected in the first seeding scenario, but for larger values of \(R_{0}\), the second scenario is more dangerous. We find that the switchover phenomenon is amplified by the geometric nature of the underlying network and confirm our results via mathematically rigorous proofs, by mapping the network epidemic processes to bond percolation. Our results expand on the previous finding that, in the case of a single seed, the first scenario is always more dangerous and further our understanding of why the sizes of consecutive waves of a pandemic can differ even if their epidemic characters are similar.