Overview of the action's implementation for the 2nd reporting period
Substantial progress can be reported on several of the sub-topics. The extension of graph limit theory to graphs with intermediate complexity, which leads to the study of Markov spaces, has been reported in several papers, two published, and two posted on the Arxiv and submitted for publication. A main result, to be followed up, was the axiomatization of subgraph densities, and a construction satisfying these axioms.
Research on the network model of disease propagation has been carried on. Two papers have been published, and two further papers exploring the mathematical background of our previous observations and simulation results are being prepared, along with a further paper connecting disease preparation to graph limit theory.
The study of physical networks (networks in real space whose nodes and edges have volumes) has been continued in cooperation between the CEU and Rényi teams, and it has lead to a manuscript submitted to PNAS. A next goal will be to explore the mathematical background, based on surprising observations from simulations.
Research in structural graph theory and its relations to graph limits and model theory has been carried on, including several issues in extremal graph theory and Ramsey theory that are raised by the studies in structural graph theory.
More and more branches of science recognize that networks are a substantial element of the appropriate description of the structures they study. These networks have an underlying structure, as well as a dynamics (propagation of material, information, or infection, for example). It is an important task to describe the interaction between the underlying structure and this dynamics. Better understanding of this interaction can lead to more reliable predictions on disease propagation, or better understanding of the working of the brain. The long-term objective of this project is to obtain nontrivial and important information about these interactions along the lines of real-life observations, simulations, mathematics modeling, and eventually rigorous mathematical results.
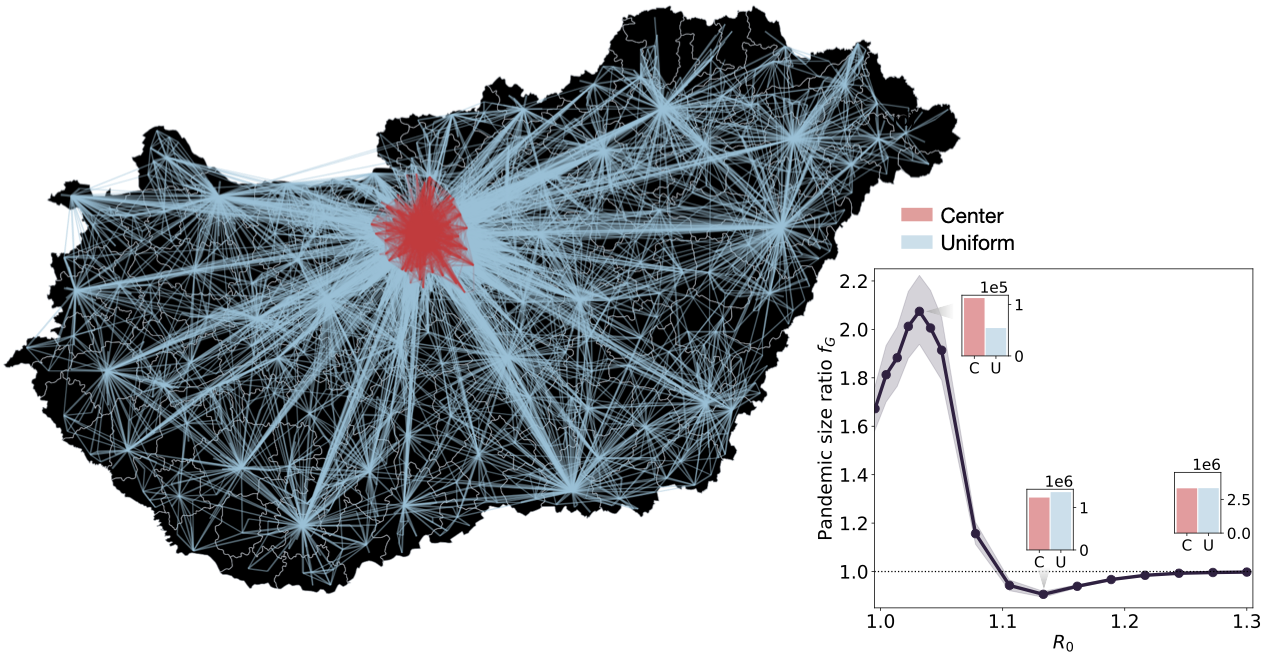
For the study of disease propagation on society networks, databases about commutation in Hungary between towns, about the spread of Covid, and about the change of behavior of people under information about the disease (awareness) have been set up, and mathematical models were formulated and programmed. Simulations on these models lead to observation of a "switch-over" phenomenon, showing a non-trivial relationship between the location of the original infection and the infection rate. Recently, an application of graph limit theory to disease propagation has been found.
To develop the mathematical foundations of network theory, convergence of graph sequences of medium density has been studied. Markov chains have been discovered to be the main ingredients of such a limit theory. This way Markov chains can be considered as generalizations of graphs, opening up a large set of problems of generalizing graph theory to Markov chains. There are several promising results about generalizing flow theory or subgraph densities. Related to the last topic, a systematic framework for combinatorial constructions of graph classes with the extension property for partial automorphisms has been developed.
Many networks in real life are "physical" (networks in real space whose nodes and edges have volume), and it is an important task to explore what combinatorial properties does this fact impose on the network. Simulations suggest interesting examples and phenomena along these lines, and a next goal will be to explore the mathematical background, based on surprising observations from simulations.
Both Markov chains (as generalizations of graphs) and physical networks are novel objects of study, and in their study one can "expect the unexpected". In dense graph limit theory, every natural limit object is "sofic" (limit of finite graphs), while for bounded-degree graphs, the soficity question is a central open problem. The intermediate case that is being developed could serve as a useful interpolation between these two extremes. The study of physical networks can lead to better understanding of the human brain, for example, by mathematically analyzing the bundling phenomenon of edges.
